https://preview.redd.it/grxkz735ekj71.png?width=567&format=png&auto=webp&s=41683460be6f1bc218aa6a4b1d488d532420e072
Non-Negative Matrix Factorization (NNMF) has many use cases, can be easily implemented in Python and is a great entry point for better understanding the concepts of machine learning and matrix multiplication.
The article below will walk you through the concept of NNMF in detail and provides a basic from scratch implementation in Python.
Hi guys, this post is to help me understand NMF better for my application.
NMF factors an input data matrix with m variables and n observations (m x n) into two lower rank matrices; a basis matrix W (m x r) and weight matrix H (r x n) both having rank r which when multiplied gives the estimated input matrix. The algorithm cannot be solved analytically because of convexity but can be solved numerically by using a multiplicative update rule.
The application is that to unmix signals which come from a linear mixing model. NMF does not require pure endmember information and it can estimate a fit for non-pure observations by setting a weight in the H matrix.
Can anyone confirm my understanding of the algorithm? Is there something that I am missing?
I am asking because I've implemented this algorithm and it cannot seem to be able to unmix my signals properly.
https://preview.redd.it/gouz4l1kul821.jpg?width=1006&format=pjpg&auto=webp&s=8cbdb41645f567524650e1fee535caf2a545a895
Paper: https://github.com/benedekrozemberczki/NMFADMM/blob/master/paper.pdf
Python: https://github.com/benedekrozemberczki/NMFADMM
Abstract:
Non-negative matrix factorization (NMF) is a popular method for learning interpretable features from non-negative data, such as counts or magnitudes. Different cost functions are used with NMF in different applications. We develop an algorithm, based on the alternating direction method of multipliers, that tackles NMF problems whose cost function is a beta-divergence, a broad class of divergence functions. We derive simple, closed-form updates for the most commonly used beta-divergences. We demonstrate experimentally that this algorithm has faster convergence and yields superior results to state-of-the-art algorithms for this problem.
It’s becoming increasingly apparent that the advances of our digital age are making a dramatic impact within the field of New Testament textual criticism. Computer processing can perform analysis that would have previously been impossible. At the same time, this also puts a new requirement on textual critics to be versed in the realm of computer science. Joey McCollum is one such practitioner, and his newly published article in Andrews University Seminary Studies introduces a powerful new tool for the work of textual criticism. In short, it effectively solves the problem of text-types. While some have called for the abolition of text-types, these groupings have potential and recognized value if they can be firmly established. For instance, text-types can simplify the text critic’s task by grouping manuscripts into families that share distinct readings. When you’re attempting to determine the genealogical flow of readings within the manuscript tradition, working with text-types or families is more manageable than working with thousands of individual manuscripts. Text-types can also aid our understanding of transmission history, and improve our knowledge of individual manuscripts. This article presents a method that makes classifying manuscripts into text-types a simple and objective task.
In his article, “Biclustering Readings and Manuscripts via Non-negative Matrix Factorization,” Joey tackles the problem of assigning manuscripts to families or text-types—or clusters, as they are called in his paper, based on shared readings.1 With so many variants, it can be challenging to assign a manuscript to a specific family when some of its readings may be typical of one family, while others may be typical of another. In other words, how much do two manuscripts have to share in common to be considered part of the same cluster? And then, when you throw in the problem of contamination, the challenge becomes increasingly difficult. This is where non-negative matrix factorization or NMF comes in. The user feeds their collation data into the program, in the form of a data table, and in a matter of minutes, the computer spits out two new data tables, one that reveals how strongly each reading corresponds to a cluster, and another that shows how strongly each manuscript corresponds to each of those clusters. If contamination is present within a manuscript, this is reflected in the second table showing that the manuscript has an affinity to multiple clusters.
As a
... keep reading on reddit ➡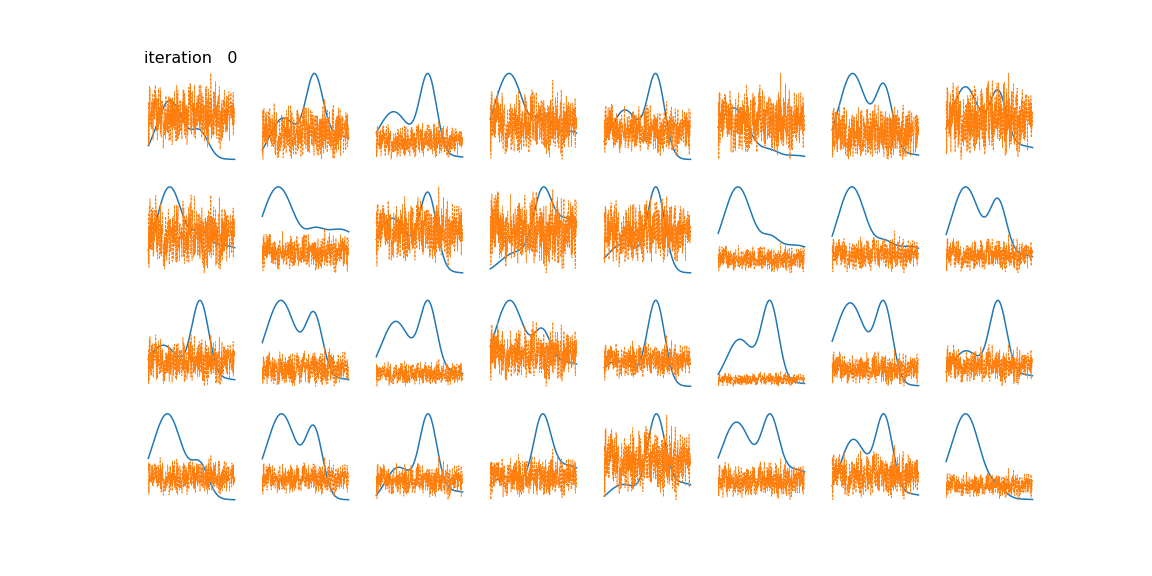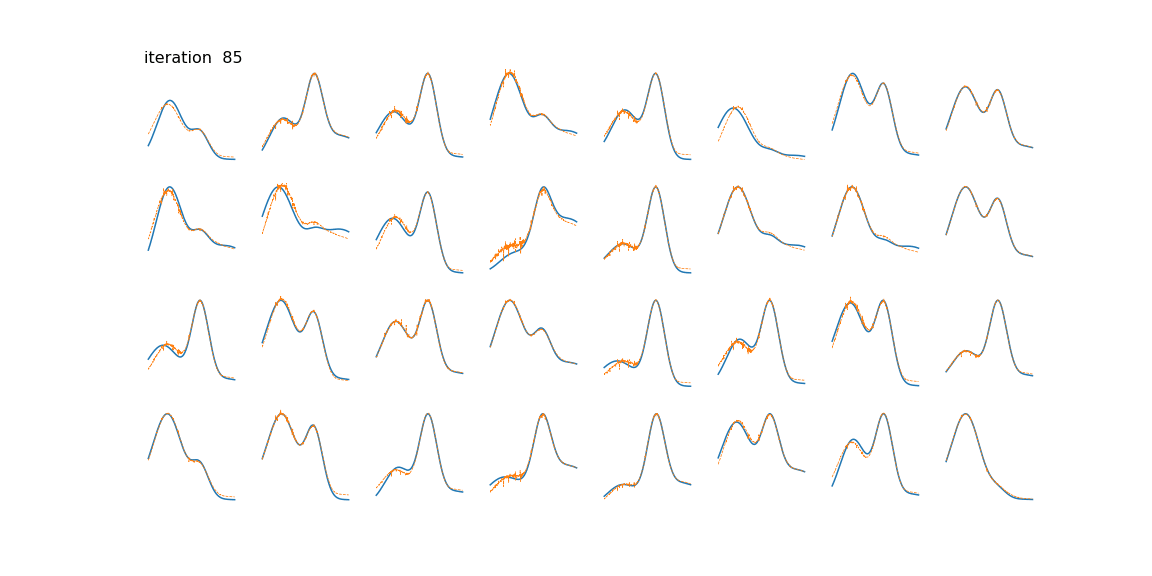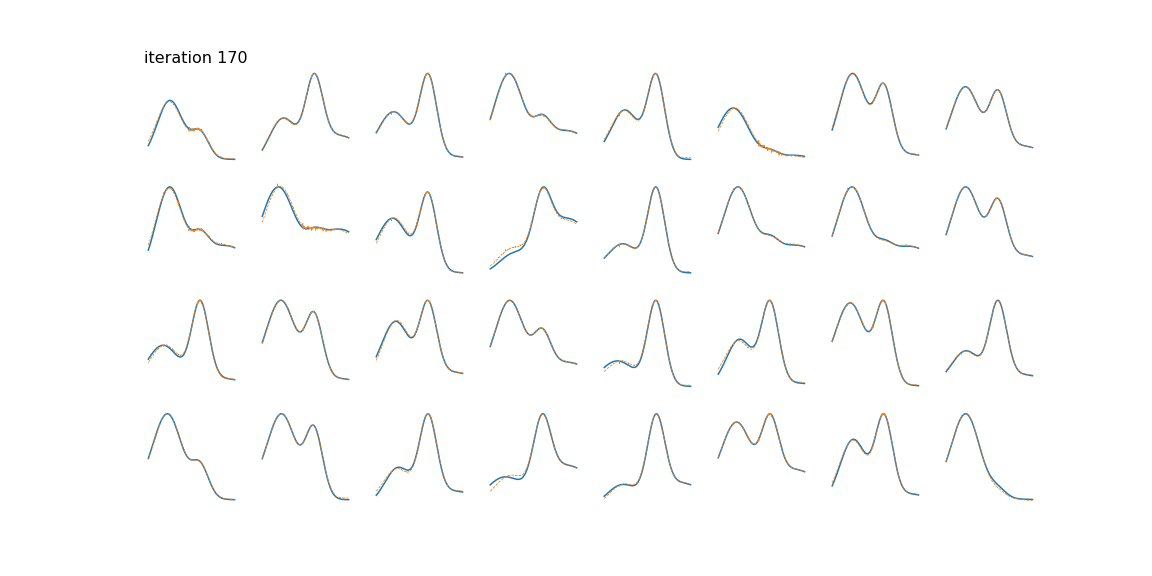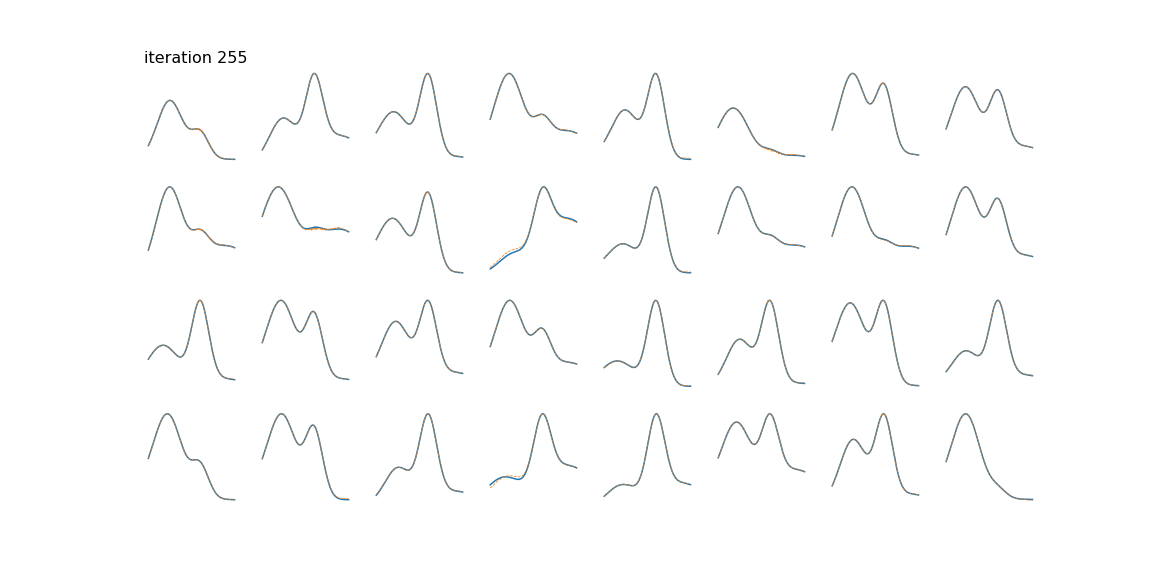
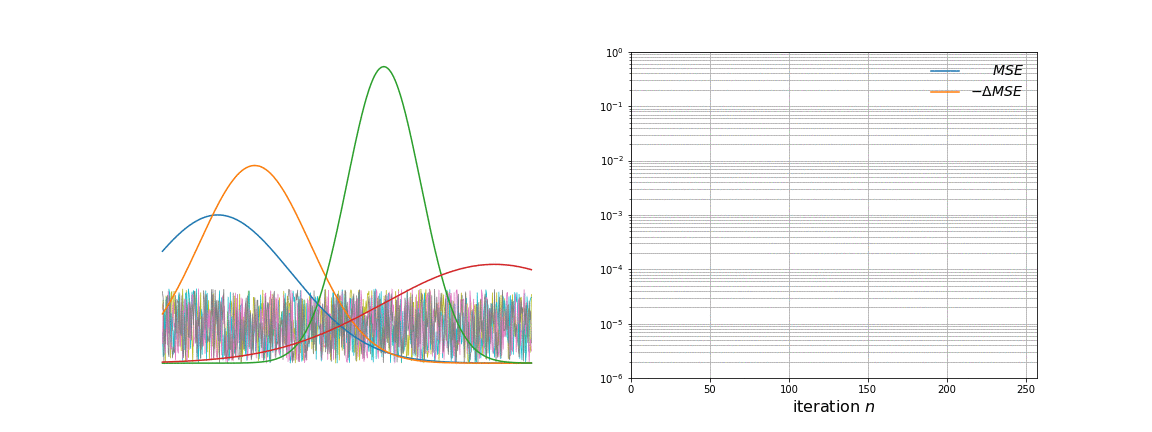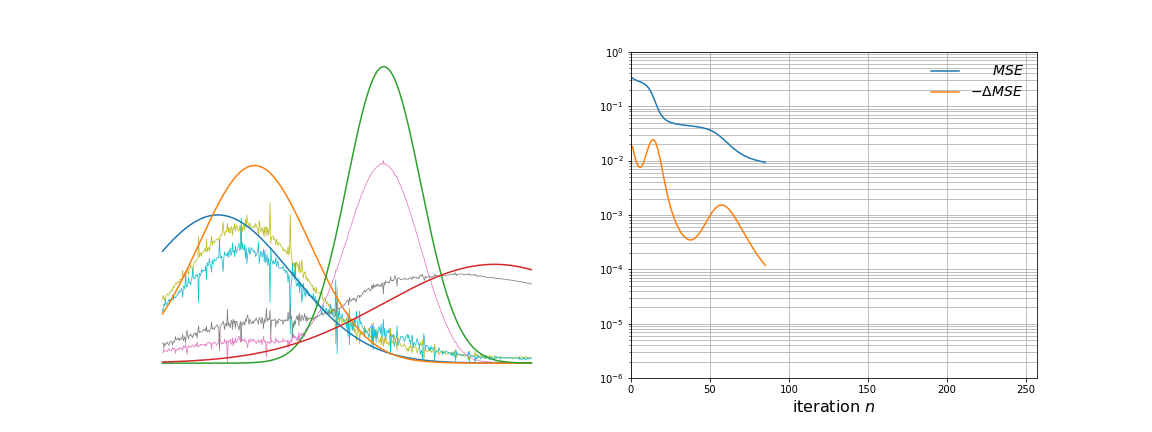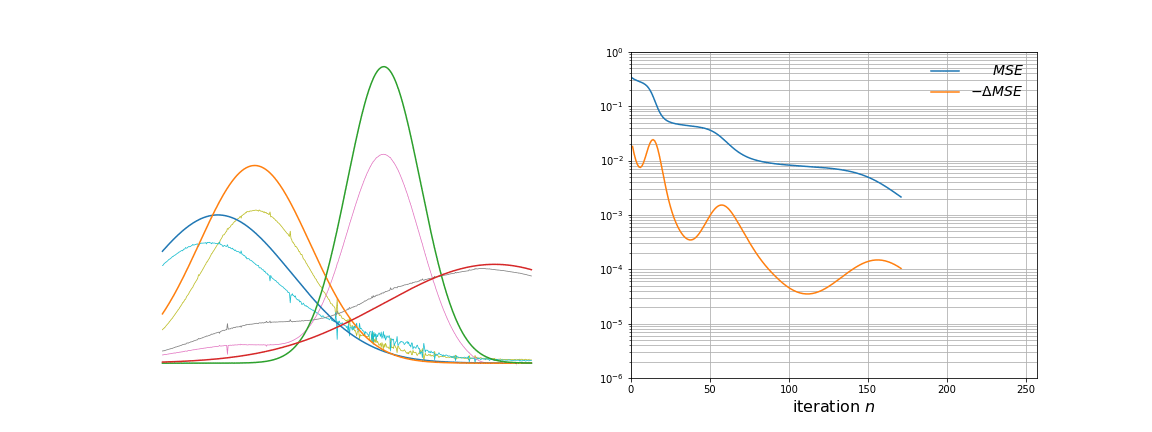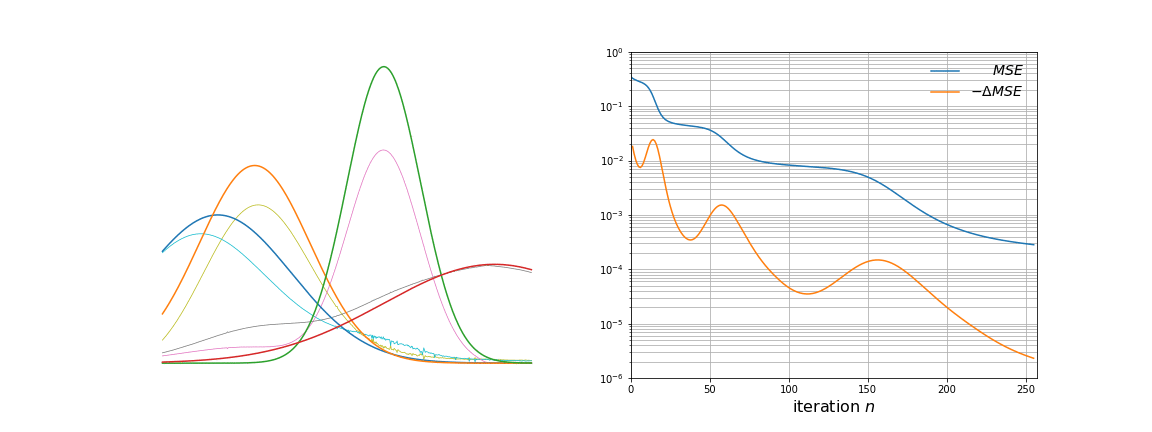
Hey guys,
I've been looking into Latent Dirchlet Allocation (LDA) https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation and NMF Non-negative Matrix Factorization (NMF) https://en.wikipedia.org/wiki/Non-negative_matrix_factorization but I'm not sure when you would choose one over the other.
I figured they have kind of the same use, producing an interpretable text representation.
Any ideas?
Here's the long-overdue discussion thread on Algorithms for Non-negative Matrix Factorization by Lee & Seung, NIPS 2000 (PDF link). This paper was awarded the NIPS classic paper award in 2013, and is one of the fundamental papers on the subject. Since it's publication, it has been cited over 3800 times (according to google).
I have come across various papers online that use NMR for estimating pitch in real time. So far, I have not found a good explanation as to why NMR is used for distinguishing pitch. Why not just use the information in the STFT (which is generally used for NMR) to get the pitch? Obviously, to track pitch in real time, the small window length does not provide enough frequency resolution to distinguish musical notes. I assume this is where NMR comes in, somehow 'increasing' the resolution...somehow...any help or pointers would be appreciated.
Does anyone know of a documented approach to optimizing the number of features to use in applying non negative matrix factorization.
(don't want features with lowly relevant items contained within, want to optimize the number of features)
A Google research team presents ALX, an open-source library that leverages Tensor Processing Units (TPUs) to enable efficient distributed matrix factorization using Alternating Least Squares.
Here is a quick read: Google Open-Sources ALX for Large-Scale Matrix Factorization on TPUs.
The paper ALX: Large Scale Matrix Factorization on TPUs is on arXiv.
A Google research team presents ALX, an open-source library that leverages Tensor Processing Units (TPUs) to enable efficient distributed matrix factorization using Alternating Least Squares.
Here is a quick read: Google Open-Sources ALX for Large-Scale Matrix Factorization on TPUs.
The paper ALX: Large Scale Matrix Factorization on TPUs is on arXiv.
A Google research team presents ALX, an open-source library that leverages Tensor Processing Units (TPUs) to enable efficient distributed matrix factorization using Alternating Least Squares.
Here is a quick read: Google Open-Sources ALX for Large-Scale Matrix Factorization on TPUs.
The paper ALX: Large Scale Matrix Factorization on TPUs is on arXiv.
