Say you have a set of 3 vectors and they're linearly independent, where the dot product of vectors x1 and x2 = 0 and the dot product of vectors x2 and x3 = 0 but the dot product of x1 and x3 DOES NOT equal 0.
To obtain an orthogonal basis can you use either vector x1 or x3? or does it have to be a specific one?
Somewhat quick question.
One of my hmw questions was to find an orthonormal basis to the space spanned by
(-1,1,0) (1,1,0) (0,0,1)
And i did this twice. The first time, i put these in a matrix and performed elementary row operations until i got to reduced row echelon form and got i,j,k as an orthonormal basis, so no need to do the process.
The second time, I did the same expect I only got to row echelon form and got a different answer.
(1/sqrt(2), -1/sqrt(2),0) (1/sqrt(2),1/sqrt(2),0) and (0,0,1)
And i put the original vectors in an online calculator and got the top (except the first vector was multiplied by negative 1) and I was wondering if there was anything wrong with going to reduced row echelon form before doing Gram-Schmidt process.
https://preview.redd.it/9fszcied1lp41.png?width=948&format=png&auto=webp&s=75f7ca35dd578413ce6987e5dad93e46b57ee0eb
https://preview.redd.it/mplksqza1lp41.png?width=923&format=png&auto=webp&s=41892535835d4434ca2183c75a49a1312f8f9435
Is my solution correct?
Hi!
I'm studying physics and tries to apply symplectic methodes in phase space.
Now, I have to do Gram-Schmidt process in symplectic phase. So, we have symplectic space which is even dimensional. That's why I've chosen four vectors with four coordinates. Now, I wonder if Gram Schmidt process is the same as in Euclidian Space but with difference in inner product? The only difference is that I have to use skew symmetric form?
Is my reasoning correct?
Sorry for mistakes. I hope you will understand me ^^
Thanks for help.
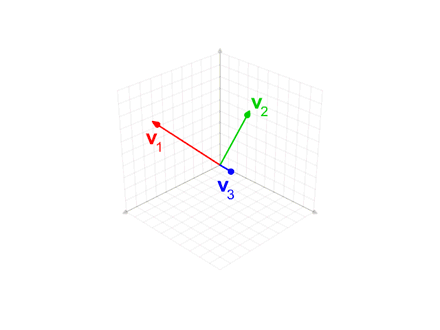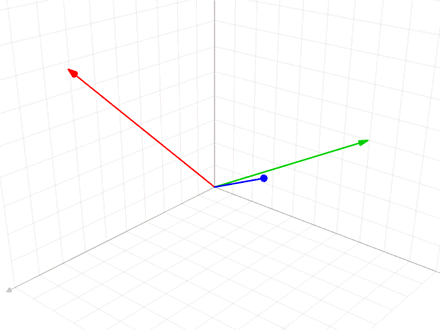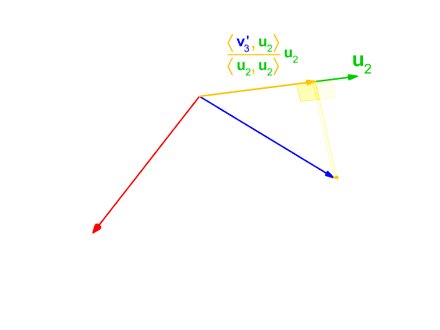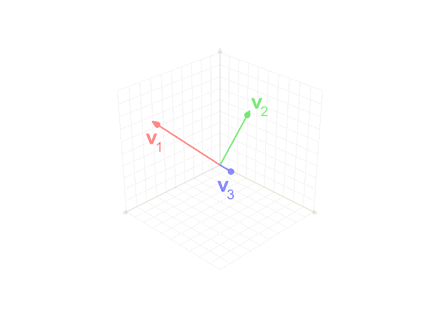
I have just been formally introduced to the Gram Schmidt process and my textbook gives the following example:
v1 = (1,1,1,1), v2 = (1,1,0,0), v3 = (3,1,1,1) - where V = Span(v1,v2,v3). In order to find a orthonormal basis U =(u1,u2,u3) we make use of the Gram Schmidt process.
u1 = (1/∥v1∥)v1 = 1/2v1 = 1/2(1,1,1,1) p1 (orthogonal projection) = 〈v2,u1〉u1 = 1/2v1
So far I understand the computation and u1 and p1 have been calculated. However, when it comes to finding u2, I cannot get my head around the process.
u2 = (1/∥v2-p1∥)*(v2-p1)=(1/∥v2-(1/2)v1∥)(v2-(1/2)v1) = 1/2(1,1,-1,-1)
I have been trying to put in the values for v2 and v1 in the equation but I get the wrong answer. (1/∥v2-(1/2)v1∥) = (1/sqrt((0,5)^2 + (0,5)^2 + (-0,5)^2 + (-0,5)^2 )) = 1 1(v2-(1/2)v1) = 1/2(v2-v1) = 1/2*(0,0,-1,-1) - which is not the answer my textbook gives, what am I doing wrong?
Hi,
I am currently learning how to do these two processes. The way I have been approaching it is to find Q (the orthonormal of a basis matrix) from A, and then using Q^T * A = R to find R.
From what I've seen online, "orthogonal" matrices are supposed to be square. Q is an orthonormal matrix I believe (as long as A is a basis matrix); but in the past I've calculated Q as a nxm matrix, which is not square.
Am I missing something? I don't think I've done anything wrong using Q^T, but if it's actually not orthogonal then Q^-1 doesn't equal Q^T.
quick edit: only square matrices can be invertible; can something be invertible and not orthogonal (or vice versa) ?
edit 2: I think I am not correctly differentiating between a matrix with orthogonal columns and an orthogonal matrix itself.
Mathematics-heavy post, I apologize in advance.
The Big Five personality traits are used in psychology to measure people's personalities. Like most concepts in psychology, its "nice" properties (objectiveness, ...) are only assumed, not proven.
Now, let's say you have a large corpus of Big Five personality test results. Taken together, they will approximate some kind of joint probability distribution, hopefully one with a defined mean and variance. Such probability distributions have nice properties, for example they support an inner product, covariance.
In linear algebra, the Gram-Schmidt process is a way to create an orthonormal basis for an inner product space. Orthonormal bases are lovely structures, though I'm having a hard time formulating why in a layman-friendly way.
So here's what I would like to do: order the Big Five traits by perceived subjectiveness, and perform Gram-Schmidt on their marginal distributions. I imagine that you'd obtain 3-5 orthonormal traits. Examining those traits might lead to some kind of insight on the human condition.
How much sense does this make? Am I completely crazy?


I'm studying for my lineair algebra test for next monday, but i'm having problems with the Gram-Schmidt process.
Take this question for example:
Determine for every eigenvalue the orthonormal basis for the associated eigenspace.
Given matrix A:
3 2 1
2 0 -2
1 -2 3
For starters I need to determine if every column is linearly indepent, which it is. Then I determine the eigenvalues with corresponding eigenspaces, which are the following:
eigenvalue = 4, 4, -2
x1 = [2 1 0]^T
x2 = [1 0 1]^T
x3 = [-1 2 1]^T
So now i have these eigenvectors which I can use in the Gram-Schmidt process right? With the following formulas:
v1 = x1
v2 = x2-(x2v1/v1v1)v1
v3 = x3-(x3v1/v1v1)v1 - (x3v2/v2v2)v2
So i did this for every vector and this matrix is my result:
2 1 -1
1 -2 2
0 5 1
Which then should be normalised to get the orthonormal basis. But this doesn't seem to be correct, could someone explain to me what i'm doing wrong?
Sorry I don't have a concrete example. But if I have a non-orthogonal basis and I convert it to an orthogonal basis does that mean that I am increasing the space that is spanned?
Hoping to get a hand with this problem. I have a solution, but I'm not sure if it's correct.
This is the question: http://imgur.com/izC8pBU,bkM1y52#1
It basically asks to use Gram Schmidt, but as an added wrinkle the function in question is a definite integral.
I think I have a solution, but I'm a little unsure whether I did v2 right.
http://imgur.com/izC8pBU,bkM1y52#0
Appreciate any help.


In the realm of infinite, separable inner product spaces, you can prove the existence of a maximal orthonormal sequence using the Gram-Schmidt Procedure.
The construction of a maximal, orthonormal sequence starts with an infinite sequence that is dense in the space from which we choose linearly independent vectors from which we construct orur basis. Does this implicitly require use of the use of the axiom of choice or are they two unrelated ideas?
I'm one that has to understand a process before I commit it...my gratitude to this board, now i have a question. I have acculated 3oo plus grams of MHRB POWDER. i plan on 3 1oo gram extracts, or do I do 6 50 gram extractions for me gain in the experience? passing along the way my results and how it worked out , for your reading pleasure course. oh the costs of research.........
Hi all, I was wondering if I can get some help on these problems.
The functions appear to be orthogonal since the integral[0,1] of (t*cos(2*pi*t)) is 0. I got u1 = t*sqrt(3) and u2 = sqrt(2)*cos(2*pi*t) when doing Gram-Schmidt since the proj term <v2, u1> = 0 due to the integral...is this on the right track? And for problem 3, I would think the vectors are still the same even when switching the order.
https://preview.redd.it/tn4t2zfmt8471.png?width=920&format=png&auto=webp&s=0bc7e89c09abdcec2a364db2f89c49eee5a2bc4b
https://preview.redd.it/vhzo61e06rt21.png?width=1196&format=png&auto=webp&s=960d018396bc77c0971ca019e00fdf77169eb619



